Öznur MUT SAĞDIÇOĞLU, PhD, Cryptography Researcher/Consultant at TÜBİTAK BİLGEM Blockchain Research Laboratory.
Edwards-curve Digital Signature Algorithm (EdDSA) is a signature algorithm scheme using a variant of the Schnorr signature based on twisted Edwards curves. It aims to have a design to deliver higher performance than existing digital signature schemes while maintaining robust security. This scheme was created by a team including Bernstein et al. in 2011, [Ber+12]. EdDSA is a deterministic signature meaning that we always get the same signature for the same private key and message, whereas ECDSA is non-deterministic which was proposed around 2001 by Johnson et al. [Jhon+01].
A threshold EdDSA is a signature scheme where a group of parties collectively compute a signature without learning the private key. In a (t, n)-threshold signature scheme, n parties hold key shares, and any subset of t parties can generate a signature, but no group smaller than t parties can perform this task. The parties all want to sign the same message m, naturally, they agree on an elliptic curve over a finite field, the same base point G on the curve, and a cryptographic hash function Hash.
Threshold key generation for EdDSA consists of the secret sharing of both the private signing key and a random secret nonce across multiple parties, enhancing security and eliminating single points of failure. Thus, a threshold EdDSA signing can be based on a DKG-based (Distributed key generation) approach. A verifiable DKG allows each party to see the commitments of all shares and confirm their validity.
As a result, the commitment to publicly shared nonces and their verification by all parties is particularly crucial. Because there is an attack that exploits the absence of nonce commitment within EdDSA threshold protocol. The vulnerability was first demonstrated through an attack on the CoSig algorithm by Drijvers et al. in 2018 [Dri+19]. As a result, it is observed that this attack can also be applied to Schnorr, EdDSA, and Musig signature schemes. This writing provides a detailed analysis of the application of this attack to the threshold EdDSA signature scheme.
In a general view of the attack, due to the absence of commitment and verification of nonces, an attacker can wait for nonces from other parties and then he find an evil/malicious nonce. As a result, using this evil nonce, he can sign any message he wants, and according to the attack, this message need not be known by the other parties. In other words, the attacker can perform signature forgery without other parties’ knowledge. To find such an evil nonce relies on Wagner’s Generalized Birthday Attack, as described in [Wag02].
The Attack
If the commitment of shared nonces and their verification is missing, then an adversary has the potential to lead other parties into signing something they didn’t intend.
Let’s assume there are three parties in the protocol to facilitate the explanation of the attack. The naming of these parties shall be as follows: Alice, Bob, and Carol. Let’s also assume that Carol is the attacker. Let (d, D = dG) represent the aggregated private and public key pairs.
The attack works as follows.
- Carol opens k concurrent signing sessions with Alice and Bob. She pro-
poses k messages {m1, m2, …, mk} which Alice and Bob would be perfectly agreeable to sign. The number k will be discussed in Wagner Generalized Birthday Algorithm section. - Carol waits for Alice and Bob to share their public nonces

with Carol in every one of the signing sessions.

where rai and rbi denote Alice and Bob’s secret nonces for signing session i.
3. Carol chooses randomly a nonce rc ∈ Zn and generates its point on the
curve Rc = rcG.
4. Carol uses Wagner’s algorithm (see Wagner Generalized Birthday Algorithm section) to find k different curve points {X1, X2, …, Xk} such that for the evil challenge e′ for its evil message m′ can be written as

and D is the aggregated public key. The evil nonce R′ is the sum of Alice
and Bob’s public nonces and Carol’s nonce Rc.
5. Each Xi is hashed with the message mi and produces a challenge

for each signing session i.
6. Due to Wagner’s algorithm, the sum of all ei hashes equals another hash
which Carol has chosen based on the evil message m′ which Alice and Bob
never see.
7. Since there is no validation of public nonces in the protocol, Carol can see Alice and Bob nonces and can produce evil nonces Rci. Carol calculates
a set of nonces {Rc1, …, Rck} one for each signing session

8. Alice and Bob upon receiving Rci, will compute the aggregate nonce

9. Carol can convince Alice and Bob to sign {m1, m2, …, mk} with the aggregated nonces {X1, X2, …, Xk} chosen by Carol. I know it is not an easy
job, but it is not impossible!
10. After that, Carol awaits k pairs of partial signatures

where wa = λa.da and wb = λb.db, and da and db are secret shares of Alice
and Bob, respectively [Int]. D is the aggregated public key.
12. Carol sums Alice and Bob’s signature shares from k signing sessions to
create a forged signature s′ which is valid for the evil message m′, D and
the evil nonce R′.
Forged Signature:
13. Carol adds her signature share

14. Since

15. Thus s′ can be written as

16. Recall that the evil nonce is defined as
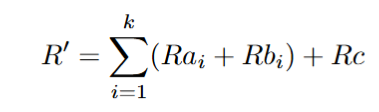
Although Carol does not know

she assumes that it is a discrete logarithm of R′. Now the secret nonce
is

17. Now substitute r′ into the signature equation to show the aggregated
signature is

and call wa + wb + wc as d, [Int].
Thus, (R′, s′) is a forged signature of the evil message m′ with the public
key D and
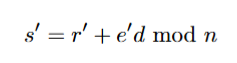
Verification:
The signature for the evil message m′ and the public key D is (R′, s′).
18. Calculate H(R′||D||m′) which is exactly e′.
19. Calculate s′G and R′ + e′D. If they are equal then the signature is valid.
Wagner Generalized Birthday Algorithm
It is time to explain how we use Wagner’s Generalized Birthday Algorithm in the attack above.
An adversary can adaptively choose its shared R-value to determine the
aggregated R-value after seeing shared nonce values from all other signing parties. Exploiting the attack involves solving the Generalized Birthday Problem, which can be done with subexponential complexity using Wagner’s algorithm, [Wag02].

Carol finds k distinct points (some set of nonces) X1, X2, .., Xk on the curve
such that for each signing session they combined with D and {m1, m2, .., mk} hash into the challenges e1, e2, .., ek. Their sum will be the evil challenge e′ = e1 + e2 + .. + ek, see the Attack section in Step 4.
For Wagner’s algorithm, some lists are defined to create the evil challenge as wanted:
1. Carol generates k − 1 lists {L1, L2, .., Lk−1}.
2. Each list Li, for i = 1, 2, .., k − 1, contains say λ hashes as follows

Namely, Li = {ei1, ei2, …, eiλ} (see Table 1) We will consider λ later.
3. Carol generates the last list Lk = {ek1, ek2, , …, ekλ} in the same way, but
this time she subtracts e′ from each hash ekj .
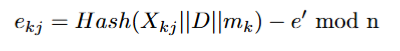
4. Carol stores Xij values in each list because she needs to define Rci, for
i = 1, 2, .., k (see the Attack section in Step 8).
As a result, Carol can find a hash value in each list and

However, how many hash values does Carol need to obtain this sum? In summary, what should the value of λ be?
The complexity
How many hashes do we need to find the following equation holds

where ej,i_j ∈ Lj?
This problem is also called the k-sum problem: Given k lists L1, L2, …, Lk
of elements drawn uniformly and independently at random from {0, 1}^n, find x1 ∈ L1, x2 ∈ L2, .., xk ∈ Lk such that x1 ⊕ x2 ⊕ … ⊕ xk = 0.
For k = 2 case, it is simply the Birthday problem. Let’s have two lists L1
and L2, each of length λ. Carol wants to find a hash chosen from each list
e1 ∈ L1 and e2 ∈ L2 so that

This equality holds with the probability

It is because the expected number of solutions in L1 and L2 will be the number of possible pairs (e1i, e2j ) times the probability that each pair could be a solution (namely, 1/n).
As a result, if λ^2 ≥ n, our expected number of solutions is at least 1, namely there is about a 50% chance that the sum of two values in the two lists will be zero. In other words, the length of each list must be at least

i.e.

For the k > 2 case, it is easy to see that a solution to the k-sum problem
exists with good probability so long as

Since there is no good algorithm with complexity

the challenge is to find a solution x1, …, xk explicitly and efficiently, [Wag02]. However, Wagner proposes an idea in [Wag02] to find a solution explicitly and efficiently. He considers the 4-list birthday problem, see Figure 1.

Given L1, .., L4 we find values x1, .., x4 that XOR is zero.

contains all pairs from L1 × L2 that agree in their least l significant bits. Each list contains about

elements.

We search matches between L12 and L34 so that x1 ⊕ x2 ⊕ x3 ⊕ x4 = 0 where lowl(x) represents the least significant bit of x. This leads to a solution to the 4-sum problem.
By the linearity of expectation
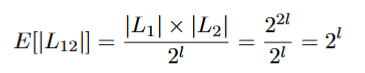
Similarly,

Any pair of elements from L12 ×L34 yields a match with probability

The expected number of elements in common between L12 and
L34 is about

To have one solution, we need

Thus, if we set l = n/3, we expect to have one solution to the 4-sum problem
with non-trivial probability. Since the size of all lists is around

the resulting algorithm can be implemented with

time and space. Wagner generalizes this idea to a k-list tree algorithm, [Wag02]. First, assume that k is a power of two. Now to solve the k-sum problem even faster than cube-root time for larger values of k, it can be extended the idea of the 4-list tree algorithm.
This will be a complete binary tree of depth lgk. At internal nodes of height
h, we use the join operator

except that at the root we use the full join operator. Each element x of an internal list Li…j contains back-pointers to elements x′ and x′′ of the two child lists used to form Li…j , such that x = x′ ⊕ x′′.
In this way, we will obtain an algorithm for the k-sum problem that requires

time and space and uses lists of size

If k is not a power of two, we work with ⌊k⌋, the largest power of two less
than k, and we use the list-elimination trick above. However, the algorithm
obtained in this way runs essentially no faster for k = 2^i + j than for k = 2^i.
Attack implementation
For the implementation, we choose an elliptic curve defined by
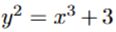
over finite field of size 101, F_101 is used. G = (1, 2) is the base point of order 17. We use SHA 256 as a cryptographic hash function.
The code is written for k = 2. According to Wagner’s Generalized Birthday algorithm, it will be enough to have λ ≥ 10. The code is written in Python.
import math
from random import randint
from ecpy.curves import Curve,Point
from ecpy.keys import ECPublicKey, ECPrivateKey
from ecpy.ecdsa import ECDSA
import random
import hashlib
import array as arr
import math
#k-sum attack on EdDSA for k=2
#y^2=x^3+3 over Z_101; G=(1,2) base point
def double(x, y, a, p):
lambd = (((3 * x**2) % p ) * pow(2 * y, -1, p)) % p
newx = (lambd**2 - 2 * x) % p
newy = (-lambd * newx + lambd * x - y) % p
return (newx, newy)
def add_points(P, Q, p):
xp, yp = P
xq, yq = Q
a=0
if xq == yq == None:
return xp, yp
if xp == yp == None:
return xq, yq
assert (xq**3 + 3) % p == (yq ** 2) % p, "q not on curve"
assert (xp**3 + 3) % p == (yp ** 2) % p, "p not on curve"
if xq == xp and yq == yp:
return double(xq, yq, a, p)
elif xq == xp:
return None, None
lambd = ((yq - yp) * pow((xq - xp), -1, p) ) % p
xr = (lambd**2 - xp - xq) % p
yr = (lambd*(xp - xr) - yp) % p
return xr, yr
def apply_double_and_add_method(G, k, p):
target_point = G
k_binary = bin(k)[2:]
for i in range(1, len(k_binary)):
current_bit = k_binary[i: i+1]
target_point = add_points(target_point, target_point, p)
if current_bit == "1":
target_point = add_points(target_point, G, p)
return target_point
def find_hash(n):
m = str.encode(str(n))
hash_value = hashlib.sha256(m).digest()
# Convert the hash value to an integer
c=int.from_bytes(hash_value, 'big')
return c
G=(1,2) #base point of order 17
def key_gen(d):
D=apply_double_and_add_method(G,d,101)
return D
#keys
da=1 #secret key of Alice
D_a=key_gen(da)
db=5 #secret key of Bob
D_b=key_gen(db)
dc=2 #secret key of Carol
D_c=key_gen(dc)
D=apply_double_and_add_method(G,(da+db+dc)%17,101)
print('Aggregated public key',D)
m = []
for _ in range(2):
random_integer = random.randint(1, 101)
m.append(random_integer)
print('Messages m1,m2 ',m) #k=2 case, we have two messages
sampleRa=[]
sampleRb=[]
ra=[]
rb=[]
for i in range(2): #k=2, each party send two nonces for each message
ra.append(random.randint(1, 101)) #secret nonce share of Alice
sampleRa.append(apply_double_and_add_method(G,ra[i],101) )
rb.append(random.randint(1, 101) ) #secret nonce share of Bob
sampleRb.append(apply_double_and_add_method(G,rb[i],101) )
print('Ra,ra',sampleRa,ra)
print('Rb,rb',sampleRb,rb)
#Attack
Rc=(1,2) #random evil nonce value of Carol
rc=1
print('Rc',Rc)
m_prime=1 # evil message
add=add_points(sampleRa[0],sampleRb[0],101)
R_agg=add_points(add_points(add_points(add ,sampleRa[1],101),sampleRb[1],101),Rc,101)
print('R_prime',R_agg)
e_prime=find_hash(int(bin(R_agg[0])[2:]+bin(D[0])[2:]+bin(m_prime)[2:],2)) %17 #evil challenge
print('e_prime',e_prime)
t=20 #\lambda
#Wagner's algorithm to find x1,x2 for k=2 case
X=[]
for i in range(t):
X.append(apply_double_and_add_method(G,random.randint(0,16),101) )
Y=[]
for i in range(t):
Y.append(apply_double_and_add_method(G,random.randint(0,16),101) )
#Lists
hashX=[]
for i in range(t):
hashX.append(find_hash(int(bin(X[i][0])[2:]+bin(D[0])[2:]+bin(m[0])[2:],2)))
hashY=[]
for i in range(t):
hashY.append(find_hash(int(bin(Y[i][0])[2:]+bin(D[0])[2:]+bin(m[1])[2:],2)))
#Wagner k-sum algorithm
for i in range(t):
for j in range(t):
if (hashX[i]+hashY[j]-e_prime)% 17 == 0:
e1=hashX[i]
e2=hashY[j]
#print('L_1',X)
print('e1, point',e1%17, apply_double_and_add_method(G,e1%101,101))
#print('L_2',Y)
print('e2, point',e2%17,apply_double_and_add_method(G,e2%101,101))
sa1=ra[0]+(e1)*da #Alice computes her signature share for each signing session
sa2=ra[1]+(e2)*da
sb1=rb[0]+(e1)*db #Bob computes her signature share for each signing session
sb2=rb[1]+(e2)*db
s_prime=(sa1+sa2+sb1+sb2+rc+(e_prime*dc)) %17 #Carol computes s_prime
print('s_prime', s_prime)
#check that s_prime is correctly evaluated
if ( (e1+e2-e_prime)%17 == 0 ) and (e_prime%17 !=0) and (e1%17 !=0) and (e2%17 !=0):
ss_prime=((ra[0]+ra[1]+rb[0]+rb[1]+rc) + (((e1+e2)%17)*(da+db)+(e_prime%17)*dc)) %17 #s'=r'+e'd
assert(ss_prime==s_prime)
#Aggregated forged signature and its verification
r_prime=(ra[0]+ra[1]+rb[0]+rb[1]+rc)%17 #r' is aggregatedly calculated
E=apply_double_and_add_method(D,e_prime%101,101)
Sum=add_points(R_agg,E,101)
S_prime=apply_double_and_add_method(G,(s_prime%101),101)
print('Signature (R_prime, S_prime)=',R_agg, S_prime)
if Sum == S_prime: #S_prime=?R_agg+e_prime*D , evil signature is verified
print('Forged signature is valid')
References:
[Wag02] David A. Wagner. “A Generalized Birthday Problem”. In: Advances
in Cryptology — CRYPTO 2002, 22nd Annual International Cryptology Conference, Santa Barbara, California, USA, August 18–22, 2002, Proceedings. Ed. by Moti Yung. Vol. 2442. Lecture Notes in Computer Science. Springer, 2002, pp. 288–303. doi: 10.1007/3-540–45708–9 \ _19. url: https : / / doi . org / 10 . 1007 / 3–540 — 45708–9%5C_19.
[Ber+12] Daniel J. Bernstein et al. “High-speed high-security signatures”. In: J. Cryptogr. Eng. 2.2 (2012), pp. 77–89. doi: 10.1007/S13389–012-0027–1. url: https://doi.org/10.1007/s13389-012-0027-1.
[Dri+19] Manu Drijvers et al. “On the Security of Two-Round Multi-Signatures”. In: 2019 IEEE Symposium on Security and Privacy, SP 2019, San Francisco, CA, USA, May 19–23, 2019. IEEE, 2019, pp. 1084–1101. doi: 10.1109/SP.2019.00050. url: https://doi.org/10.1109/SP.2019.00050.
[Int] Polynomial Interpolation. In: (). url: https://en.wikipedia.org/
wiki/Polynomial_interpolation.

