Öznur MUT SAĞDIÇOĞLU, PhD, Cryptography Researcher/Consultant at TÜBİTAK BİLGEM Blockchain Research Laboratory.
Digital asset custody involves methods for safeguarding digital assets on behalf of their owners. It can be in many forms, such as hot wallets, cold wallets, hardware wallets, and custodial services for which third-party services manage digital assets on behalf of users.
Custody primarily focuses on securely storing and managing the cryptographic keys needed to access and transfer the assets: a public key and a private key. The private key allows the asset owner to authorize transactions, serving as a verifiable proof of ownership. Given their crucial role, custody solutions must securely store these keys to ensure that only the asset owner can access them. Otherwise, if the private key is compromised or the asset owner loses it accidentally, the digital asset risks being lost or stolen.
As a result, to securely store private keys, and avoid a single point of failure, the concept of sharing custody responsibilities has drawn great attention in recent years with threshold signature algorithms based on multiparty computation (MPC).
Threshold signatures require a subset of parties, namely signatories, authorized to produce signatures on behalf of the group. The message is only considered signed if a number t, the threshold, of signers signs the message. The process is based on MPC, no single entity has full control of the key, enhancing security and resilience. In other words, these solutions ensure that the private key is never exposed at any instance of the process.
Although numerous ECDSA threshold signature protocols have been pro-
posed in the literature, this writing focuses on GG18, GG20, MPC CMP, CG-
GMP, and a Class Group-based ECDSA scheme CCLST ([GG18], [GG20], [CMP20], [CGGMP], and [CCLST], respectively). We talk about each protocol’s performance, resilience against potential attacks, and inherent complexity, evaluating their practical application for secure and efficient custody solutions in the digital asset space.
Today, various organizations and institutions are working on digital asset custody solutions using threshold signature schemes based on MPC, such as BitGo, Fireblocks, and Coinbase Custody. Selecting an optimal threshold signature scheme is important for ensuring the security and efficiency of digital asset custody. To this end, a thorough understanding of the differences between various threshold signature schemes is essential, especially for custody services looking to implement Multi-Party Computation (MPC) solutions in their custody frameworks.
This comparison helps to assist developers and researchers in evaluating these protocols to choose the most effective solution based on the specific requirements of their MPC-based custody projects.
Threshold ECDSA Protocol
A threshold signature scheme (TSS) is a signature scheme where a group of parties collectively compute a signature without learning the private key. In a (t,n) -threshold signature scheme, n parties hold key shares, and any subset of t parties can generate a signature, but no group smaller than t parties can perform this task. TSS key generation depends on distributed key generation (DKG) protocol, in this way, no party can learn the private key when they generate key shares.
ECDSA (Elliptic Curve Digital Signature algorithm)
ECDSA is an Elliptic Curve Digital signature algorithm. While DSA is based on arithmetic operations modulo over a prime number, ECDSA uses elliptic curve operations over finite fields. Requiring shorter key lengths and being more efficient than its predecessors, ECDSA has become the signature scheme of choice, powering major systems like Bitcoin and Ethereum.
Let F_q be a finite field of order q, and H be a hash function for embedding messages into the field of q elements. Let (G,g,q) denote the group-order-generator tuple associated with the ECDSA curve. We use the multiplicative notation for the group operation.
The ECDSA signature for a secret key x ∈ F_q and the message m is
r is the x-projection (mod q) of the point
and k is uniformly random nonce in F_q.
The verification algorithm accepts signature (r, s) with the message m and
the public key Q = x × G.
The verifier calculates
If r = x_1, then the signature is valid otherwise it is invalid.
Difficulties in threshold computing
ECDSA signature depends on a random nonce k, which must be kept secret and used only once per signature. Threshold ECDSA protocols require the participants collaboratively to compute
without revealing k and kx without compromising the signature private key x.
Directly sharing information about k exposes it, which can lead to the compromise of the private key x. Indeed, if the nonce k is reused or leaked for two different messages m not equal to m’, one can have the private key as
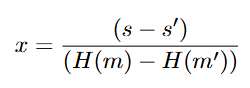
Moreover, it was shown that even less than 1 bit of bias in k is enough to recover the whole private key, [LadderLeak20]. This situation can happen in real life, for example, a random number generator can generate a number whose most significant bit(s) may be the same for different messages. Knowing such a vulnerability in a random generator, for example, an attacker can collect many signatures to recover the signature’s private key.
Thus, modular inversion in a threshold setting is inherently challenging. Since no single party should know the full nonce k in a threshold setting, the nonce must be generated collaboratively in a distributed manner.
Let us see how this can be done. Assume that each party P_i has a secret nonce share k_i and a mask γ_i of k_i. Let
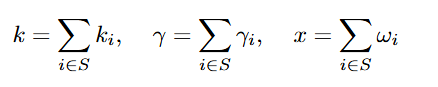
where S represented signatories whose number is at least t and
and δ_i are Lagrangian coefficients.
Parties first jointly compute
In the signing protocol, each part commits its public value γ_i × G, and so at
the end, they jointly calculate the inverse of k by multiplying the following values
At this point, how can every pair of signatories calculate k_iγ_j and k_jγ_i without disclosing their secrets k and γ ? This is solved by a protocol that helps to convert multiplicative shares into additive ones, the Multiplicative-to-additive share conversion protocol (MtA), [Gil99].
P_i calculates k_iγ_j and has a share
where α_ij is the share of P_i and β_ij is the share of P_j. The same idea is applied to kx.
MtA protocol’s security depends on the use of the homomorphic encryption scheme. Since it is based on homomorphic encryption, it can be used with Pailler-based or class group-based encryption.
If Paillier encryption is used, like RSA, each party holds its own Paillier key. This key should be generated appropriately and verified for validity by other parties, which can be done using zero-knowledge range proof. Otherwise, if the Paillier key is not properly generated or verified, there’s a risk of exposing the private signing key, which could compromise the security of the entire threshold signature protocol, [MY23]. Thus, a threshold ECDSA based on Paillier encryption needs many zero-knowledge proofs to show that each party’s Paillier key is correctly generated, that the encrypted values must be a given range, and that the encrypted value corresponds to a discrete logarithm of some known public value, like in [CMP20] and [CGGMP].
There are protocols like GG18, GG20, CMP, and CGGMP using a combination of Paillier encryption and threshold ECDSA. These protocols are typically designed to ensure security and correctness even if a small number of participants act maliciously, called a dishonest majority.
Paillier encryption efficiently hides the message m ∈ Z_N, where N is Pallier modulus, assuming that computing the N th residuosity classes of ciphertexts, c mod N^2, is hard, [Pai99]. The homomorphic property of Pailler encryption for any two messages m, m′ ∈ Z_N means that
Second, MtA can be used with class groups of imaginary quadratic fields, [CCLST]. In other words, encryption is done in a class group, which is a group of unknown order. Since class groups have an unknown order, threshold ECDSA protocols based on class group encryption eliminate the need for a trusted third party directly. Furthermore, as this signing protocol does not use the Paillier modulus, we avoid the necessity for the zero-knowledge proofs. Another advantage of this approach is that the message space is the same as the order of the elliptic curve, which further reduces the need for additional zero-knowledge proofs that should be used in a Paillier-based scheme, [MP21].
Therefore, these aspects contribute to significantly lower communication
costs. Moreover, as noted in [CCLST], a class group-based scheme with the same security level significantly reduces bandwidth consumption compared to other approaches. However, since the signing protocol is based on a group of unknown orders, it is needed zero-knowledge proof for the correction of the encryption in this scheme.
MtA (Multiplication to Addition)
Threshold ECDSA protocols are based on a core protocol, Multiplication to Addition (MtA). MtA protocol as noted above, converts multiplicative shares into additive ones without revealing the shares and is based on homomorphic encryption. Thus, in this section, a Paillier or a class group-based encryption can be used for the encryption operation.
Let S ⊆ [1..n] be the set of players participating in the signature protocol
(|S| > t). Before the MtA, each party has a secret share of the private key (signing key). They choose randomly their secret share x_i from F_q .
Let each party P_i select a nonce share k_i and a mask γ_i in the finite field of order q. Define
Note that
Each party commits the public value of γi × G at the beginning of MtA. This commitment is a non-malleable equivocable commitment, [CGGMP].
Every pair of signatories P_i and P_j engages in a multiplicative-to-additive
share conversion protocol for the shares k_i of the party P_i and γ_j of the party P_j. Then MtA protocol can create an additive form without revealing the multiplicative shares.
MtA protocol to calculate k_iγ_j securely as follows:
- Party P_i encrypts k_i with its Paillier public key: Enc_i(k_i), and sends it to P_j.
- Since P_j does not know the private key, it can not learn k_i. However, due to the homomorphic encryption, P_j can calculate with the public key of P_i
a randomly chosen element β_ij in F_q . P_j sends it to P_i.
- P_i decrypts it modulo q and calls it
- Note that P_i can never learn γ_j because P_i does not know β_ij (called a
mask). - Thus, two parties P_i and P_j jointly compute the additive shares of the
product so that
where k_i is the secret key share of P_i and γ_j is the secret share of P_j .
The protocol runs MtA twice between P_i and P_j so that the following additive shares are calculated:
The signing protocol for threshold ECDSA protocol also uses MtA to compute the additive shares of kx.
When MtA protocol runs, each party P_i has the following additive shares:
where
δ_i are Lagrangian coefficients.
Using the public values parties jointly compute
and
Thus, when the message is known, each party P_i has signature shares
The signature will be
GG18 and GG20
GG18 and GG20 are threshold ECDSA protocols created by Rosario Gennaro
and Steven Goldfeder, [GG18], and [GG20]. Both GG18 and GG20 are Paillier-
based threshold ECDSA protocols, [Pai99].
GG18 was the first protocol that supports t ≤ n threshold signatures with
no trusted third party, where t is the threshold and n is the number of parties. However, the communication cost of GG18 is high, namely 9 rounds for signing.
Thus, the authors design a fast protocol, GG20 with adding some crucial properties: noninteractive online signing and identifiable abort. If something goes wrong in an identifiable abort due to malicious intent or an unintentional mistake, who did it can be easily recognized and held accountable. GG20 is faster because most of the computations are done during the offline stage, when the message is known, parties only calculate one scalar multiplication in one round.
GG18 and GG20 schemes require each participant to prove that their
publicly disclosed N satisfies the square-free property. However, verifying square-freeness alone does not ensure that N is a valid Paillier modulus. If the Paillier modulus contains small prime factors, then the signature private key will be exploited. The attack done by the Fireblocks team which exploits the full private key by using only 16 signatures and the Chinese Remainder theorem, is called the 6ix1een attack, [MY23]. Moreover, in the same paper, the Death by 1M cuts attack targets the old version of GG18 and GG20 where the beta parameter in MtA is chosen from {1, …, N } and again, Paillier modulus has small factors, [MY23]. This attack also retrieves the private key again using relatively more signatures, depending on the number of signatories.
GG18 and GG20 use the MtA protocol and MtAwc (MtA with check). In
MtA, a party’s inputs are not verified, and in MtAwc a public value adds a
verification step with an abort. However, even if these protocols use some zero-knowledge proofs, MtA and MtAwc, in GG18 and GG20 are still vulnerable to an attack where the encrypted values of Paillier encryption are not in some range with proof, [MP21]. Although this attack does not lead to the exposure of the full private key, it must still be regarded as a serious security concern. As a result, in [MP21] the authors of CGGMP add zero-knowledge range proof for the parameters used in MtA.
In the latest attack article about the threshold ECDSA protocol based on Paillier encryption, it is stressed that MPC-CMP and CGGMP protocols with zero-knowledge range proofs for checking those values have no vulnerabilities, [MY23].
MPC-CMP and CGGMP
Fireblock uses MPC CMP as a threshold signature algorithm. It has an open-source code, so everyone can check that the protocol is mathematically safe and sound. CGGMP protocol’s key generation is a 3-round protocol. Instead of Feldmann VSS like in GG18 and GG20, each party proves by Schnorr’s zero-knowledge proof that it knows the secret signing private key share.
Key-Refresh and auxiliary information is a 3-round protocol. Auxiliary in-
formation means each party has a correct Paillier modulus and Ring Pedersen parameters. In this stage, due to the mentioned attacks, parties must prove that the Paillier modulus is a Paillier Blum modulus, and can be factored into exactly two prime factors which are not small, [MY23].
Another zero-knowledge proof is for a generation of valid ring Pedersen
parameters. As in the key generation process, the refreshed key is needed a
Shnorr’s proof of knowledge. Also, it is checked that the modulus for Paillier and ring Pedersen is bigger than a bound given in [CGGMP]. In this protocol, they use ephemeral values for the validity of the secret signing key share for each signing operation. Finally, in the key refresh, parties check the sum of public key shares is zero. For these, they can abort a corrupted party easily.
However, to reach this feature they must use quite a few zero-knowledge proofs. MPC-CMP provides a non-interactive signing capability even in the presence of an adversary that adaptively corrupts up to t = n − 1 signatories.
MPC CMP is analyzed within the Universally Composable (UC) Security
framework, [CMP20]. The protocol achieves an ideal threshold signature functionality within the UC framework, operating in the global random oracle model. Its security is based on the Strong RSA assumption, the semantic security of Paillier encryption, and a slightly enhanced version of existential unforgeability for ECDSA, [CMP20].
The authors of two independent works, GG20 and CMP, collaborated on
a paper CGGMP that has enhanced the CMP protocol lately. CGGMP features a key refresh mechanism. For the key refresh phase, the authors use DH-style encryption because it is more efficient than Paillier and its security proof is much more easier under DDH assumption, [CGGMP]. In addition, due to the Paillier commitment and a noninteractive zero-knowledge proof, parties are confident that their output is well formed at the end of the pre-signing phase.
CCLST 2023
The ideal class group (or class group) of an algebraic number field K is the
quotient group C = JK/PK where JK is the group of fractional ideals of the
ring of integers of K, and PK is its subgroup of principal ideals, [CCLST]. In
CCLST, it is formalized that a group exists in which the decisional Diffie-Hellman problem is hard, whereas it contains a subgroup in which the discrete logarithm problem is easy. And it is denoted by a DDH Group G = ⟨g⟩ with an easy DL Subgroup F = ⟨f ⟩, [CCLST]. Also, they proposed a linearly homomorphic encryption scheme, called CL framework, that relies upon such a group and the authors prove its security. The encryption for a message m is given by
for a random r, the public key pk is h.
CL framework is semantically secure under chosen plaintext attacks (ind-cpa). The ind-cpa security relies on the HSM (Hard Subgroup membeship assumption), [CCLST]. Another assumption for the security of this protocol is the low-order element assumption which improves the efficiency of the zero-knowledge proofs needed in the protocol. The third assumption is the strong root assumption similar to the Strong RSA assumption. For strong RSA, this involves factoring the modulus. The strong root problem in class groups requires computing the class number, for which the best-known algorithms have worse complexity compared to integer factorization algorithms.
To put it more briefly and clearly, a DDH group with an easy DL subgroup exists in the class group of imaginary quadratic fields, and it allows us to create a linearly homomorphic encryption scheme, that is why this encryption can be used in MtA.
In more detail,in the key generation phase of the threshold ECDSA scheme, parties generate jointly g_q whose order is unknown to all parties. Then they generate the group generator
for a DDH group G where f is the generator of F, a DL subgroup of G, [CCLST]. After the group is generated, the parties independently create their encryption key pairs
Then they collaboratively generate the signing key pairs using Feldman VSS and Shamir Secret sharing, [DKG].
The signing protocol proposed by Castagnos et al. closely follows the structure of GG20 substituting Paillier encryption with the class group encryption.
As mentioned, since the message space is the same as the order of the elliptic curve q, the MtA protocol does not need zero-knowledge proof which exists for MPC CMP and CGGMP. This yields a significant bandwidth improvement. However, as it is used a class group of unknown order, the protocol must include zero-knowledge proofs to ensure the correctness of the encryptions.
To identify a corrupted party, or for identifiable abort, the protocol employs the same approach as outlined in the GG20 protocol. However, due to the class-group-based encryption, they need to design new zero-knowledge proofs that enable the simulator to complete the proof successfully without compromising the overall efficiency of the protocol.
In the latest update of class group-based threshold ECDSA, many features
are added by the authors, [CCLST]. The protocol is a noninteractive, maliciously secure, full-threshold ECDSA protocol. It has identifiable aborts, adaptive security for t = n−1, and proactive security.
Last but not least, the authors achieve their goal that the protocol improves upon existing Paillier-based implementations, achieving similar objectives while reducing bandwidth consumption by a factor of up to 10, [CCLST].
To Sum Up
All threshold signature schemes -GG18, GG20, CMP, CGGMP, and CCLST-
operate under the assumption of a dishonest majority. All schemes mentioned so far can be adapted to a protocol without a trusted third party. Thus, each party generates its own secret share, functioning both as a dealer and as a recipient in the key generation process for the ECDSA signature algorithm.
GG18, GG20, and CCLST use distributed key generation methods: Feldman
Verifiable Secret Sharing (VSS) and Shamir Secret Sharing, to generate the
signature private key. In the CMP and CGGMP, each party generates its secret shares and uses Schnorr’s proof to verify knowledge of the secret share associated with their public share.
As mentioned above there are two kinds of encryption in threshold signature protocol: one is based on Paillier encryption and the other is based on class groups of imaginary quadratic fields.
For the Paillier encryption, the Paillier modulus must be chosen properly.
An attack proposed by the Fireblocks team demonstrates practical exploitation of the private key, [MY23]. There is no mechanism in GG18 and GG20, like a range-proof check, for detecting small factors of N (factors of size 2⁸⁰ or smaller are considered critical vulnerabilities) and it is the product of exactly two primes.
Therefore, when generating a new Paillier (RSA) modulus N, the following zero-knowledge range proofs must be provided to verify
While threshold ECDSA signature schemes provide enhanced security, they
may still be vulnerable to evolving attacks. Consequently, either the signature keys or encryption keys could be at risk of compromise over time. To achieve proactive security parties periodically engage in a key-refresh protocol. This approach helps maintain security over time by refreshing keys without changing the public key, thus preventing gradual leakage and ensuring the protocol remains secure against long-term threats.
CMP and CGGMP include a periodic key refresh mechanism, resulting in
full proactive security, [CMP20] and [CGGMP]. CCLST also adds a key refresh mechanism for the full threshold, t = n − 1 in the latest version of the paper, [CCLST].
In the CCLST scheme, the key setup/refresh explicitly requires parties to
generate new encryption key pairs, namely each party P_i generates the public key share
where g is public, [CCLST].
Thus, since there is no need to generate a new key or refresh key, the CCLST key setup/refresh protocol works much faster. It is given that for n = 5 and a 112-bit level of security, the total data sent and received between players in the key refresh protocol is 15 times less than one in CGGMP, [CCLST].
To minimize computational costs, protocols with the latest updates implement a presigning or offline signing stage after the key setup/refresh stage. After these steps, when the message is available, parties non-interactively compute the signature shares and broadcast this share to all signatories. This stage takes only one round to complete the signing.
Another important thing in threshold cryptography is accountability. A
threshold signature protocol achieves accountability by identifying corrupted signatories in case of failure to generate a valid signature. It is called identifiable abort in [CGGMP], [GG20] and [CCLST].
Now we are ready to list the properties of each threshold ECDSA scheme.
GG18
• Multiparty signatures for any t ≤ n.
• Dishonest majority
• Paillier-based encryption
• Security assumptions: DDH and Strong RSA assumptions, [GG18]
• Static adversaries ( the adversary must choose which players to corrupt at the beginning of the protocol. )
• Key generation: Feldman VVS and Shamir SS
• MtA share conversion protocol.
• Non-malleable equivocable commitments, [GG18].
1. Key generation: 3 rounds
2. Signing: 9 roundsGG20
• The successor to GG18.
• A non-interactive threshold ECDSA protocol: when the message is known, only one noninteractive round for signing.
• Multiparty signatures for any t ≤ n.
• Dishonest majority.
• Paillier-based encryption.
• Security assumptions: Enhanced ECDSA, DDH, strong RSA.• Static adversaries and rushing adversaries (the adversary gets to speak last
in a given round and, in particular, can choose his message after seeing
the honest parties’ messages. )
• Key generation: Feldman VSS and Shamir’s SS.
• MtA conversion protocol.
• Non-malleable equivocable commitments.
• Identifiable abort, both in key generation and signing.
• Rounds:
1. Key generation: 3 rounds,
2. Signing: 7 rounds (including 1 online)MPC CMP
• A non-interactive threshold ECDSA protocol.
• Multiparty signatures for any t ≤ n.
• Dishonest majority.
• Paillier-based encryption.
• Security analysis in the UC framework.
• Security assumptions: Strong RSA, semantic security of the Paillier encryption, and enhanced ECDSA.
• Static adversaries for t < n and adaptive adversaries for t = n − 1.
• A key refresh mechanism.
• Full proactive security.
• The MtA share conversion protocol.
• Paillier as non-malleable equivocable commitment
• Ring Pedersen commitments
• Rounds:
1. Key generation : 3 rounds
2. Auxiliary Info. & Key Ref: 2 rounds
3. Signing: 3 rounds presigning + 1 round online signing.CGGMP
• Joint work of the authors of GG20 and CMP.
• A non-interactive threshold ECDSA protocol.
• Multiparty signatures for any t ≤ n.
• Dishonest majority.
• Paillier-based encryption.
• Security analysis in the UC framework.
• Adaptive adversaries for t = n − 1.
• Identifiable abort.
• Online/Noninteractive signing.
• Key refresh mechanism.
• Proactive security.
• Security assumptions: Strong RSA, DDH, enhanced ECDSA.
• Static adversaries for t < n and adaptive adversaries for t = n − 1 as long as at least one party remains uncorrupted between any two consecutive key .
• Full proactive security.
• MtA share conversion protocol based on Paillier and zero-knowledge range proofs.
• Paillier as non-malleable equivocable commitment
• Ring Pedersen commitments.
• Rounds:
1. Key generation: 3 rounds.
2. Auxiliary Info. & Key Ref: 3 rounds
3. Signing: 3 rounds presigning + 1 round online signingCCLST
• A noninteractive threshold ECDSA protocol.
• Multiparty signatures for any t ≤ n.
• Dishonest majority.
• Class group-based encryption.
• Provable security. Simulation-based and game-based proofs.
• Adaptive security for t = n − 1 and proactive security.
• Identifiable abort .
• Key generation: Feldman VSS and Shamir’s SS
• Non-interactive signing.
• Key refresh mechanism.
• Security assumptions: Hard subgroup membership assumption, the low-order assumption, and a strong root assumption for class groups.
• MtA share conversion protocol.
• Non-malleable equivocable commitments
• Rounds:
1. Setup (threshold computation of the group generator ): 5
rounds,
2. Key generation: 4 rounds,
3. Key refresh: 3 rounds,
4. Signing : 6 +1 (online round)
An approximate communication cost of these schemes is given as a Figure in [CGGMP]. In parentheses below, it is provided concrete estimates given in [CGGMP] for the curve secp256k1 (i.e., the Bitcoin curve and q = 256) and log(N ) = 2048 for 112-bit security for Paillier.
GG18: 43520 bits ( 7 KiB)
Class group-based threshold ECDSA: 25600 bits (3.5 KiB)
CGGMP: 119040 bits (15 KiB)
Conclusion
GG18 and GG20 are implemented by various vendors and open-source projects, such as Binance bnb-chain, ING Bank (open source project), ZenGo (open source project), and Safeheron, [MY23]. The protocols are vulnerable to some attacks mentioned above. The issue arises from the absence of correct generation and validity checks for the Paillier modulus and the parameters used in the MtA share conversion protocol. As a result, when custody uses them, they need proof to verify the Paillier modulus and the parameters used in MtA like in [CGGMP].
In CMP and CGGMP protocols, such vulnerabilities have been addressed using zero-knowledge range proofs. However, employing a large number of range proofs significantly increases communication costs.
To minimize bandwidth consumption and reduce the overhead introduced by zero-knowledge range proofs, an alternative method based on class group encryption has been proposed.
Although reducing bandwidth consumption is advantageous, class group-based homomorphic encryption relies on highly complex mathematics. On the other hand, threshold signature schemes using Paillier encryption are more straightforward to implement, as they primarily involve relatively simple modular arithmetic.
References:
[Gil99] Niv Gilboa. “Two Party RSA Key Generation”. In: Advances in
Cryptology — CRYPTO ’99.
[Pai99] Pascal Paillier. “Public-Key Cryptosystems Based on Composite
Degree Residuosity Classes”. In: Advances in Cryptology — EURO-
CRYPT ’99.
[CL15] Guilhem Castagnos and Fabien Laguillaumie. “Linearly Homomor-
phic Encryption from DDH”. In: IACR Cryptol. ePrint Arch. (2015).
[GG18] Rosario Gennaro and Steven Goldfeder. “Fast Multiparty Thresh-
old ECDSA with Fast Trustless Setup”. In: Proceedings of the 2018
ACM SIGSAC Conference on Computer and Communications Secu-
rity, CCS 2018.
[Ara+20] Diego F. Aranha et al. “LadderLeak: Breaking ECDSA with Less
than One Bit of Nonce Leakage”. In: CCS ’20: 2020 ACM SIGSAC
Conference on Computer and Communications Security, Virtual Event,
USA.
[CMP20] Ran Canetti, Nikolaos Makriyannis, and Udi Peled. “UC Non-Interactive,
Proactive, Threshold ECDSA”. In: IACR Cryptol. ePrint Arch. (2020).
[GG20] Rosario Gennaro and Steven Goldfeder. “One Round Threshold ECDSA with Identifiable Abort”. In: IACR Cryptol. ePrint Arch. (2020).
[CGGMP] Ran Canetti Rosario Gennaro Steven Goldfeder Nikolaos Makriyannis Udi Peled. “UC Non-Interactive, Proactive, Threshold ECDSA
with Identifiable Aborts”. In: CCS ’20: 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, USA.
[MP21] Nikolaos Makriyannis and Udi Peled. A Note on the Security of
GG18. 2021.
[MY23] Nikolaos Makriyannis and Oren Yomtov. “Practical Key-Extraction
Attacks in Leading MPC Wallets”. In: IACR Cryptol. ePrint Arch. (2023).
[CCLST] Guilhem Castagnos Dario Catalano Fabien Laguillaumie Federico
Savasta Ida Tucker. “Bandwidth-efficient threshold EC-DSA revisited: Online/offline extensions, identifiable aborts proactive and adaptive security”. In: Theor. Comput. Sci. 939 (2023).
